如何理解伽罗瓦群？_II32资讯下载站

为什么多项式域扩张会导致伽罗瓦群缩减？

为什么有的多项式在原本的域上的伽罗瓦群的阶数并不等于n！？

为什么分圆多项式的伽罗瓦群是循环群？

galois群就是某多项式的根排成一列的换位方式的集合。

例如某5次多项式有5个根，叫做

a,b,c,d,e

现在排成一列，然后打乱，再重新排成一列，这就是一个换位动作。这样的动作有多个，收集成一个集合，就叫做galois群。

凡是看到galois群，在心里就念成换位集，不是侯君集也不是双堆集，是换位集，这样念就通顺了。

再细讲应说galois群是换位集的子集合。例如某多项式有4根，其中两个很像男生，两个很像女生，现在排一条线坐下，但男生想坐在一起，女生想坐在一起。

忽有大风吹，4人乱跑再坐下，那就不是任意坐了，而是喜好并肩坐，是任意坐的子集。任意坐方法数是4*3*2=24，并肩坐方法数是2*2*2=8，较少。

=== === === ===

细讲，就举例 x^4 +5 x^2 +6=0 , 它的解是

+- sqrt(-2) , +- sqrt(-3) , 简称为 a, -a, b, -b, 按照位置1,2,3,4 先坐好。

接着， a 说要和 b 换位，西格瑪搬家公司 sig 说可以，但他会把全部的有理系数串串 q0 + q1 a - q2 a + q3 b - q4 b

都全部换位，问a同意吗? a 说可以。

那sig(a*a)=sig(a)*sig(a)同意吗? a说可以，

那么 sig(-2)=sig(a)*sig(a) 可吗？a說可以，

那么 sig(-2)= b* b 可吗？ a说可以，

但搬家公司不乐意了，他说 -2是有理数，他搬不了， -2 只能搬到-2，不能搬到 bb，于是这搬迁被拒绝，只a和b换位被拒绝。原来这搬家公司是伽氏集团(galois group)的。

=== === === ===

又细讲，例如 x^4 -1=0 , 它的解是

{1, i, ii, iii}, 按照位置1,2,3,4 先坐好。

接着， i 说要和 ii 换位，其它不换。西格玛搬家公司 sig 说可以试试，但他说好将把 sig(a b)，搬到 sig(a) sig(b)，问 i 同意吗? i 说试试。

那么sig(i*i)=sig(i)*sig(i)同意吗? i说可以，

那么 sig(i i)= i i * i i , 同意吗？i 說可以，

那么 sig(-1)= -1 * -1 同意吗？ i说可以，

但搬家公司不乐意了，他说 -1是有理数，他搬不了， -1 只能搬到-1，不能搬到 +1，于是这搬迁被拒绝，只搬i和 ii 换位被拒绝。原来这搬家公司是伽氏集团(galois group)的。

一个多项式方程在不同的数域中有不同的形态。

多项式在它的分裂域里分解成一次因式的乘积。并且用符号替换因式中的常系数时，可以明确判定数域的维数，以及方程系数在其中可以有多少种排列方式而代数结构不变（自同构也就是元素间的加减乘除关系不变）。所以伽罗瓦群被用来描述这种性质

可解方程的分裂域，可以通过每次添加当前数域中某个元素的根式进行扩域。

从而形成一个类似洋葱的多层结构的扩域。

并且由于每层扩域是通过添加单个元素的根扩张而来，所以扩域相对于原数域的商群是交换群。

这种结构就被称为可解群

一个代数方程，如 $ax^{2}+bx+c=0$ ，它的根能不能用系数通过加减乘除以及开根号等表示出来，这件事情是很神奇的。我们知道，二次方程的根可以表示出来为 $x_{1,2}=\frac{-b\pm\sqrt[2]{b^{2}-4ac}}{2a}$ .

这件事情神奇在哪里呢？我们来看一个N次代数方程 $a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 = 0,\quad a_n\neq 0,$ 我们知道系数和根的一个逆向关系（也就是维达定理Vieta's formulas）

$x_{1} + x_{2} + \cdots + x_{n} = -\frac{a_{n-1}}{a_n}$

$\sum_{1 \le i < j \le n} x_i x_j = \frac{a_{n-2}}{a_n}$

$\sum_{1 \le i < j < k \le n}x_i x_j x_k = -\frac{a_{n-3}}{a_n}$

...

$x_1 x_2 \cdots x_n = (-1)^n\frac{a_0}{a_n}$

为了方便起见，我们给出一个N=3的情况

$x_1+x_2+x_3=-\frac{a_2}{a_3 }$

$x_1x_2+x_1x_3+x_2x_3=\frac{a_1}{a_3 }$

$x_1x_2x_3=-\frac{a_0}{a_3 }$

也就是说， N次代数方程等价于N个方程组，这个方程组不是线性的。我们要通过系数a反解出x

当然线性方程组这件事情是可以做到的，这就是线性代数里面学的。

非线性方程组一般是做不到的，这是感觉。但是我们的方程组有很好的形式，你观察就会发现，用x表示a的时候，a都是关于x的对称函数，也就是任意置换xi和xj，a都是不变的。例如 $x_1+x_2+x_3=-\frac{a_2}{a_3 }$ 中，任意改变 x_i 和 x_j 等号的左边都不变。

我们要回答，这样形式（Vieta's formulas）的方程组，能不能求解呢？超越普遍的非线性方程组，反解x呢？

毕竟三次方程和四次方程组都是可以求解的。我们截图给你们看看三次方程的求根公式，参考【数学女孩】这本书

这种能不能的问题就是“池塘里面有没有鱼的问题”非常重要，非常漂亮，非常有挑战。

伽罗瓦的一生，参考【数学女孩】这本书，真的是天才的一生，因为他解决了上面这个问题。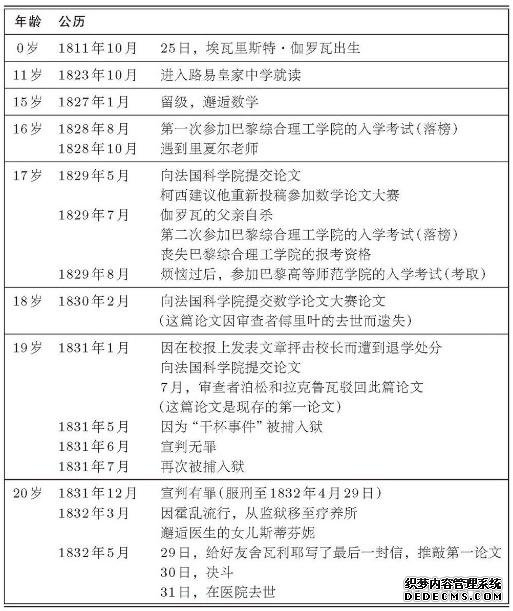

复杂的数学都是从简单的例子出发，别看数学家说得很普遍，他们的例子就是那么屈指可数的几个

考虑多项式方程， x^2-9=0 ，我们知道它可以写成 (x-3)(x+3)=0 ，这种就是因式分解的形式。

我们再看多项式方程 x^2-2=0 ，它可以写成上面那种因式分解的形式吗？你知道答案，是 $(x+\sqrt{2})(x-\sqrt{2})=0$ 。

我们再看 x^2+1=0 , 它可以写生上面的因式分解的形式吗？你知道答案，是 (x+i)(x-i)=0

上面的三个例子其实说明了一件事情，就是第一个可以在有理数范围内实现因式分解，写成 (x-3)(x+3)=0 ；第二个是不可以在有理数的范围内因式分解的，如果要因式分解，我们至少要学了无理数 $\sqrt{2}$ 才行，才能写成是 $(x+\sqrt{2})(x-\sqrt{2})=0$ ；同样的，第三个需要再复数的范围内才能因式分解。

所以我们知道了一件事情，一个多项式能不能实现因式分解，也就是说，写成 $\prod_{i=1}^{N}(x-x_i)=0$ 的形式。一旦写成了这种形式，我们就能直接给出多项式方程的根了。

在这里你也可以看到，把 x^2-2=0 因式分解需要无理数，但是不需要所有的无理数，比如，我们不需要 $\sqrt{3}$

我们只需要在这样一个集合{ $\alpha+\beta\sqrt{2}$ }，其中 $\alpha$ 和 $\beta$ 都是有理数即可。因为这个集合中的元素满足加法封闭，乘法也封闭，它形成了一个数域。就像有理数集合一样，他们里面的元素关于加法和乘法都是封闭的，例如，你任意从这个集合里面取两个数，他们的和或者积都在这个集合里面。

我们有一个结论出现了，一个非常普遍的多项式， $f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$ ，我们先假设所有的系数是有理数（其实本来是整数，但是我们总可以把除以一个 ,所以所有的系数都变成了分式的形式，也就是有理数），这个要实现因式分解，就必须考虑超越有理数的范围，例如在一个无理数，或者复数范围内考虑才行。不然不能写成 $\prod_{i=1}^{N}(x-x_i)=0$ 的形式。但是巧妙就巧妙在，我们需要的这个范围也不用大到整个无理数或者整个复数范围，只需要在一个刚好包含了所有根的数的集合（数域）中考虑就行。

我们把系数所处的域，就是系数所在的那个数的集合（满足加法和乘法封闭）记为Q

我们把所有的根都包含在内的那个最小的域，也是数的集合（满足加法和乘法封闭）记为E，这个E叫做这个多项式的分裂域。当然我们尽量不引入新的名词，因为每次说包含所有根的最小的数域，这个有点麻烦，我们就把他定义为多项式的分裂域

你想，如果对于普遍的多项式， $f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$ ，在那个包含了它所有根的数域（）

(责任编辑：admin)

搜索

热门标签:

如何理解伽罗瓦群？